Random Variables: Discrete and Continuous
Introduction
Random variables form the foundation of probability theory and statistical analysis, serving as mathematical tools that quantify uncertain outcomes. Whether you’re a statistics student, data scientist, or researcher, understanding the distinction between discrete and continuous random variables is crucial for proper data modeling and analysis. This comprehensive guide explores both types of random variables, their properties, applications, and the mathematical frameworks that govern them.
What Are Random Variables?
A random variable is a variable whose value is determined by the outcome of a random event. It’s essentially a function that assigns numerical values to the outcomes of a random experiment.
Types of Random Variables
Random variables are classified into two main categories:
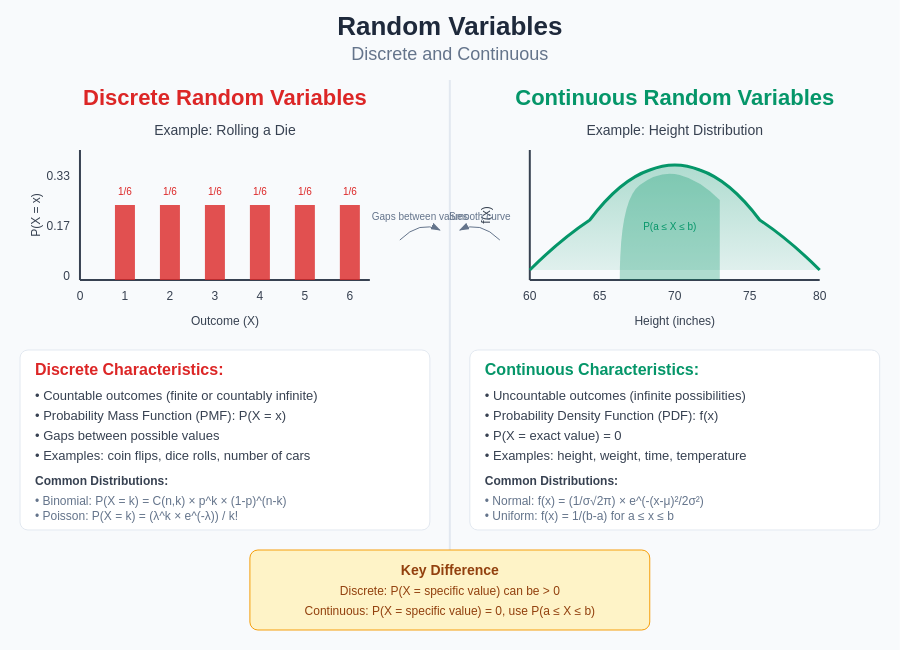
- Discrete random variables – Take on countable, distinct values
- Continuous random variables – Can take on any value within a range
Let’s explore each type in detail.
Discrete Random Variables
Definition and Properties
A discrete random variable can only take on distinct, separate values. These values are typically countable, meaning they can be listed or enumerated.
Key properties:
- Values are distinct and separate
- Can be finite or countably infinite
- Often represented as whole numbers
- Probability is assigned to each specific value
Probability Mass Function (PMF)
The distribution of a discrete random variable is described by its Probability Mass Function (PMF), denoted as P(X = x) or f(x).
PMF properties:
- Non-negative: P(X = x) ≥ 0 for all x
- Sum of probabilities equals 1: ∑P(X = x) = 1
- P(X = x) represents the probability that X takes the value x
Common Discrete Distributions
| Distribution | Formula | Applications | Parameters |
|---|---|---|---|
| Bernoulli | P(X=1) = p, P(X=0) = 1-p | Binary outcomes (success/failure) | p = success probability |
| Binomial | P(X=k) = (n choose k)p^k(1-p)^(n-k) | Number of successes in n trials | n = number of trials, p = success probability |
| Poisson | P(X=k) = e^(-λ)λ^k/k! | Rare events in fixed time/space | λ = average rate |
| Geometric | P(X=k) = (1-p)^(k-1)p | Number of trials until first success | p = success probability |
Example: Coin Flips
When flipping a fair coin three times, the random variable X might represent the number of heads observed. X can take values 0, 1, 2, or 3.
The probability mass function would be:
- P(X=0) = 1/8 (no heads)
- P(X=1) = 3/8 (one head)
- P(X=2) = 3/8 (two heads)
- P(X=3) = 1/8 (three heads)
Continuous Random Variables
Definition and Properties
A continuous random variable can take on any value within a range or interval. Unlike discrete variables, continuous variables can take on an infinite number of possible values, including fractions and irrational numbers.
Key properties:
- Values form a continuum
- Can take any value within a range
- Cannot be counted, only measured
- Probability of any single point is zero
Probability Density Function (PDF)
Continuous random variables are characterized by a Probability Density Function (PDF), typically denoted as f(x).
PDF properties:
- Non-negative: f(x) ≥ 0 for all x
- Total area under the curve equals 1: ∫f(x)dx = 1
- P(a ≤ X ≤ b) = ∫[from a to b]f(x)dx
- P(X = a) = 0 for any single point a
Common Continuous Distributions
| Distribution | Applications | Parameters | |
|---|---|---|---|
| Normal | f(x) = (1/σ√2π)e^(-(x-μ)²/2σ²) | Natural phenomena, measurement errors | μ = mean, σ = std. deviation |
| Uniform | f(x) = 1/(b-a) for a≤x≤b | Equal likelihood in range | a = minimum, b = maximum |
| Exponential | f(x) = λe^(-λx) for x≥0 | Waiting times, lifetimes | λ = rate parameter |
| Gamma | Complex formula | Waiting times for multiple events | α = shape, β = scale |
Example: Height Measurements
Human height in a population is typically modeled as a continuous random variable because it can take any value within a range (e.g., someone could be 168.3721… cm tall).
Key Differences Between Discrete and Continuous Variables
Understanding the differences between discrete and continuous random variables is essential for selecting appropriate statistical methods.
| Characteristic | Discrete Random Variables | Continuous Random Variables |
|---|---|---|
| Values | Countable, distinct values | Uncountable, can be any value in a range |
| Distribution Function | Probability Mass Function (PMF) | Probability Density Function (PDF) |
| Probability of a Single Point | Can be positive | Always zero |
| Mathematical Representation | Summation (∑) | Integration (∫) |
| Graphical Representation | Bar graph, histogram | Smooth curve |
| Cumulative Distribution | Step function | Smooth function |
Applications in Statistics and Data Science
Hypothesis Testing
Random variables are crucial in hypothesis testing, where we test assumptions about populations using sample data.
- Discrete case: Testing proportions or counts (e.g., testing if a coin is fair)
- Continuous case: Testing means or variances (e.g., t-tests for comparing group means)
Regression Analysis
In regression models, the dependent variable can be either discrete or continuous, determining the appropriate modeling approach:
- Discrete outcome: Logistic regression, Poisson regression
- Continuous outcome: Linear regression, polynomial regression
Machine Learning
The type of random variable influences the choice of machine learning algorithms:
- Classification problems: Often involve discrete target variables
- Regression problems: Typically involve continuous target variables
Mathematical Foundations
Expected Values
The expected value (mean) of a random variable represents its long-term average over many repetitions.
For discrete random variables: E(X) = ∑x·P(X=x)
For continuous random variables: E(X) = ∫x·f(x)dx
Variance and Standard Deviation
Variance measures the spread or dispersion of the random variable around its mean.
For discrete random variables: Var(X) = ∑(x – E(X))²·P(X=x)
For continuous random variables: Var(X) = ∫(x – E(X))²·f(x)dx
The standard deviation is the square root of the variance: σ = √Var(X)
Transformations of Random Variables
When we apply a function g to a random variable X to create a new random variable Y = g(X), the distribution changes accordingly:
For discrete random variables: P(Y=y) = ∑P(X=x) for all x where g(x) = y
For continuous random variables: f_Y(y) = f_X(g⁻¹(y)) · |dg⁻¹(y)/dy|
Real-World Examples
Discrete Random Variables in Practice
- Customer counts: The number of customers entering a store each hour
- Quality control: The number of defective items in a manufacturing batch
- Telecommunications: The number of calls received by a call center
- Electoral systems: The number of votes received by candidates
Continuous Random Variables in Practice
- Physical measurements: Height, weight, temperature
- Financial markets: Stock prices, exchange rates
- Environmental science: Pollution levels, rainfall amounts
- Engineering: Component lifetimes, material strength
Frequently Asked Questions
What is the difference between a random variable and a probability distribution?
A random variable is a function that assigns numerical values to outcomes of a random experiment. A probability distribution describes how the probabilities are distributed over the values of the random variable.
Can a random variable be both discrete and continuous?
No, a random variable is either discrete or continuous, not both. However, some distributions, like the mixed distribution, combine both discrete and continuous components.
How do you determine if a random variable is discrete or continuous?
A random variable is discrete if its possible values form a countable set. It’s continuous if it can take any value within a range. Consider what values the variable can take – if you can list them all or count them, it’s discrete; if it can be any value within a range, it’s continuous.
What is the relationship between PMF and PDF?
The PMF (for discrete variables) gives the probability of each specific value, while the PDF (for continuous variables) gives the relative likelihood of values falling within a range. The integral of the PDF over a range gives the probability of the variable falling within that range.
How are random variables used in Bayesian statistics?
What is the difference between a random variable and a probability distribution? A random variable is a function that assigns numerical values to outcomes of a random experiment. A probability distribution describes how the probabilities are distributed over the values of the random variable.
Can a random variable be both discrete and continuous? No, a random variable is either discrete or continuous, not both. However, some distributions, like the mixed distribution, combine both discrete and continuous components.
How do you determine if a random variable is discrete or continuous? A random variable is discrete if its possible values form a countable set. It’s continuous if it can take any value within a range. Consider what values the variable can take – if you can list them all or count them, it’s discrete; if it can be any value within a range, it’s continuous.
What is the relationship between PMF and PDF? The PMF (for discrete variables) gives the probability of each specific value, while the PDF (for continuous variables) gives the relative likelihood of values falling within a range. The integral of the PDF over a range gives the probability of the variable falling within that range.
How are random variables used in Bayesian statistics?
In Bayesian statistics, random variables represent both the data and the unknown parameters. Prior distributions are assigned to parameters, and Bayes’ theorem is used to update these distributions based on observed data, resulting in posterior distributions.

